【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】

03-07 6419阅读 0评论

​

🕺作者： 迷茫的启明星

😘欢迎关注：👍点赞🙌收藏✍️留言

🎃相关文章

【数据结构从0到1之树的初识】

【数据结构】带你学会二叉树的链式存储的前中后序遍历，遍历推导及利用队列实现二叉树的层次遍历。

🏇家人们，码字不易，你的👍点赞🙌收藏❤️关注对我真的很重要，有问题可在评论区提出，感谢阅读！！！

持续更新中~

​【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第1张【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第2张【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第3张

前言

前面一篇讲述了树，包括树的定义·相关概念和树的存储结构等，今天将讲述二叉树的的理论及相关应用·堆排序·TOPK问题。

1.二叉树简介

1.1二叉树定义

一棵二叉树是结点的一个有限集合，

该集合或者为空，

或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

二叉树的特点：

  • 二叉树是每个结点最多有两个子树的树结构。
    • 即二叉树不允许存在度⼤于2的树。
    • 二叉树的子树有左右之分，其子树的次序不能颠倒。

      1.2现实中的二叉树

      【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第4张

      在普通人眼中，可能会说这树真标准，都分两个叉，

      而在程序员眼中这就是一棵完美的二叉树，

      经历·职业·价值等等不同，

      导致不同人的眼中就是不同的世界，

      每个人都活在自己的世界里，

      我们终其一生都在扩大自己无知的边界（像一个圆）。

      回到正题

      1.3数据结构中的二叉树

      它有五种最基本的形态：

      • 二叉树可以是空集

      • 根可以有空的左子树或者右子树

      • 左右子树都是空。只有左子树或者右子树的叫做斜树

        【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第5张

        1.4特殊的二叉树

        满二叉树：

        1. 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

        2. 也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。( k ≥ 1)

        3. 也可以这么理解，在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树。

        看你觉得哪种方式更好理解就用哪种~~~

        举例：

        【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第6张

        特点：

        • 所有的叶子节点都在最后一层
        • 所有的分支节点都有两个孩子

          完全二叉树

          1. 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。

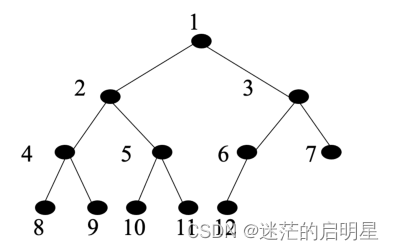
          2. 对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

          3. 要注意的是满二叉树是一种特殊的完全二叉树。

          【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第7张

          特点：

          • 所有的叶结点都出现在第k层或k－1层
          • 若任一结点，如果其右子树的最⼤层次为i，则其左子树的最⼤层次为i或i＋1
          • 前N-1层都是满的
          • 最后一层不满，但是最后一层从左到右是连续的

            引言：

            【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第8张

            【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第9张

            那么10亿个节点的完全二叉树是多少层？

            2^h -1=10^9

            结果h约为29.9，故完全二叉树应有30层。

            是不是很夸张，才30层就是10亿了，这就是指数的力量。

            下面将系统的讲述二叉树的性质。

            1.5二叉树的性质

            • 性质1：

              若规定根节点的层数为1,在二叉树的第i层上的结点最多为2^(i-1) 个。

              • 性质2：

                若规定根节点的层数为1，深度为h的二叉树至多有2^h -1个结点。

                • 性质3：

                  在一棵二叉树中，叶结点(度为0)的数目永远比度为2的结点数目多一个。

                  a. 总节点数为各类节点之和：n = n0+ n1 + n2

                  b. 总节点数为所有子节点数加一：n = n1 + 2*n2 + 1

                  故：n = n + 1

                  • 性质4：

                    若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log₂(n+1)

                    练习题：

                    1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2
3.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12
解析：
1.B
性质3
度为0的数目永远比度为2的结点数目多一个
2.A
性质3
a. 总节点数为各类节点之和：n = n0+ n1 + n2
b. 总节点数为所有子节点数加一：n = n1 + 2*n2 + 1
假设 度为0，节点数为x0
	度为1，节点数为x1
	度为2，节点数为x2
x0+x1+x2=2n
而x2=x0-1
故2*x0+x1-1=2n
2^n为2的倍数，故x1-1也应该等于2的几次方，
故x1等于1，即得度为0节点(叶子节点)个数为n
3.B
设高度为h
2^(h-1)-1 0)
	{
		if (a[child] > a[parent])
		{
			HPDataType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

                    向上调整写完了，总的插入是怎么做的呢？

                    typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void HeapPush(HP* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		size_t newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = realloc(hp->a, sizeof(HPDataType)*newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
	//上面实现过的向上调整函数
}

                    这时候就能通过插入元素来建立大堆了

                    void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}
void HeapPrint(HP* hp)
{
	for (int i = 0; i size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}
int main()
{
	int a[] = { 70, 56, 30, 25, 15, 10, 75 };
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i  

                    小堆类似，就不过多赘述了。
                     

                    2. 堆的基本操作-数据的删除
                     
 
 
                    注：删除堆顶的数据
                     
 
 
 
                    意义：上面我们了解了大堆，小堆的含义，
                    又通过堆的插入发现可通过堆选出最大值Or最小值，
                    那么每次只要我们取堆顶的元素就可以取出堆中的最大值or最小值。
                     
 

                    注意：我们对堆进行操作时，通常不改变其原有的性质，最后大堆仍是大堆，小堆仍是小堆。
                     

                    我们该怎么操作呢?
                     
 
 
                    很多人第一想法就是把堆顶取出，这是数组存储对吧，直接后面覆盖前面的元素就行了。
                    可是这样会改变堆的原有性质，不再是大堆or小堆了，那下次如果再想取最大值Or最小值岂不是又要重新建大堆or小堆？
                    嗯，不妙。
                     
 
 
 
                    所以有这么一种方法，先把堆顶的元素的值备份一下，再把最后一个元素赋给堆顶，然后向下调整
                     
 

                    向下调整是怎么样的呢？
                     
 
 
                    假如这是个大堆，现在要删除堆顶元素,
                     
 
                    然后将最后一个元素赋给了堆顶,
                     
 
                    我们要调整以后仍是大堆，
                     
 
                    那么就看此时的堆顶元素与左右孩子的比较了，
                     
 
                    举个例子：
                     
 
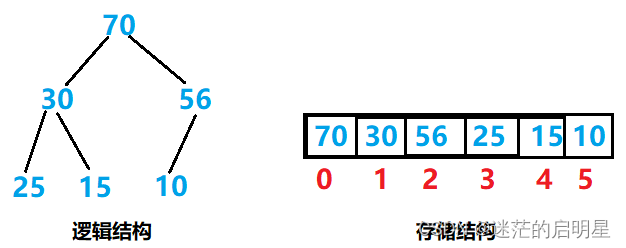
                    有这样一个堆：
                     
 
                    【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第10张
                     
 
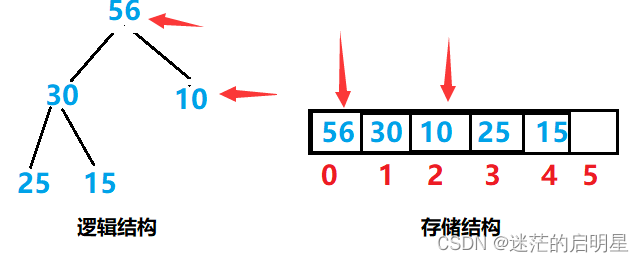
                    按照前面所说，将最后一个元素赋给了堆顶
                     
 
                    【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第11张
                     
 
                    此时已不是大堆了
                     
 
                    就该向下调整
                     
 
                    发现左右孩子都比10大，选择哪一个呢？
                     
 
                    记住一个技巧，大堆换大孩子，小堆换小孩子
                     
 
                    很简单嘛，这是大堆，如果和小孩子换了，那小孩子成了父亲，还是比大孩子小，仍然不是大堆
                     
 
                    接着上面的图示
                     
 
                    和大孩子交换
                     
 
                    【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第12张
                     
 
                    结果仍是大堆
                     
 
                    代码怎么写呢？
                     
 
                    向下调整函数：
                     
 
                    void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child  a[parent])
		{
			Swap(&a[child], &a[parent]);//交换值
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

                     
 
                    删除堆顶元素函数：
                     
 
                    bool HeapEmpty(HP* hp)
{
	assert(hp);
	return hp->size == 0;
}
// 删除堆顶的数据
void HeapPop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	//交换堆顶与最后一个元素的值
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

                     
 
                    讲到这里是不是觉得特别简单？
                    其实后面讲述的堆排序就是利用堆的性质进行排序的，取堆顶元素而已。
                     
 

                    3.堆的应用-TOPK问题
                     

                    在N个数中找出最大的前K个 or 在N个数中找出最小的前K个
                     

                    N表示数目极多，一般认为K远小于N
                     

                    有三种方法：
                     

                    方式一：
                     
 
 
                    将N个数排降序，前十个就是最大的。
                     
 
                    最快的排序方法是快排，后面会专门讲解快排的，这里知道就好。
                     
 
                    时间复杂度：O(N*logN)
                     
 
                    太复杂了，如果数据非常多，存不下，就无法使用这个方法
                     
 

                    方式二：
                     
 
 
                    N个数依次插入大堆，Pop K次，每次取堆顶的数据。
                    时间复杂度为：O(N+logN*K)
                    这种方法也方法有一样的弊端，数据量太大，内存不够则无法计算。
                     
 

                    拓展：建堆的时间复杂度怎么算？
                     
 
 
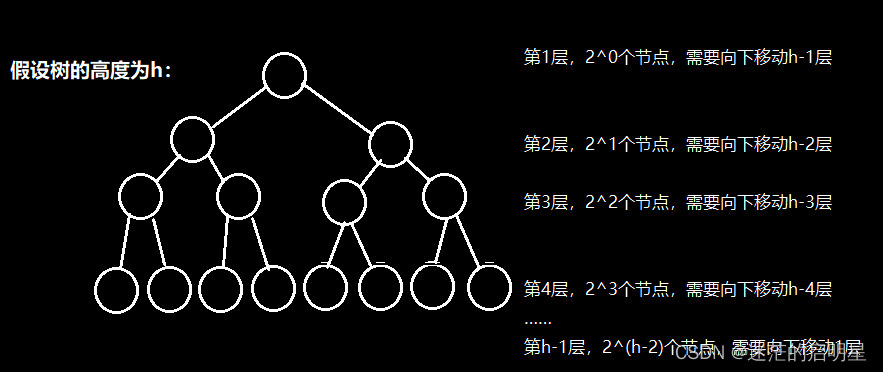
                    因为堆是完全二叉树，而满二叉树也是完全二叉树，
                    此处为了简化使用满二叉树来证明
                    （时间复杂度本来看的就是近似值，多几个节点不影响最终结果）：
                     
 
                    【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第13张
                     
 
                    则需要移动节点的移动步数为：
                     
  
  
                    T(n)=20*(h-1)+21*(h-2)+22*(h-3)+23*(h-4)+……+2(h-3)*2+2(h-2)*1 Ⅰ
                     
  
                    ​2*T(n)=21*(h-1)+22*(h-2)+23*(h-3)+24*(h-4)+……+2(h-2)*2+2(h-1)*1 Ⅱ
                     
  
                    Ⅱ-Ⅰ错位相减：
                     
  
                    T(n)=1-h+21+22+……+2^(h-1)
                     
  
                    T(n)=20+21+22+……+2(h-1)-h
                     
  
                    T(n)=2^h -1 -h
                     
  
                    n=2^h -1 h=log2(n+1)
                     
  
                    T(n)=n - log2(n+1)约等于n
                     
  
 
                    因此，建堆的时间复杂度为O(N)
                     
 

                    方式三：
                     

                    假设N非常大，内存中存不下这些数，他们存在文件中的是K个数。
                     
 
 
                    1.  
                      用前K个数建立一个K个数的小堆
                       
                    2.  
                      剩下的N-K一个数依次跟堆顶的数据进行比较
                       
                      如果比堆顶的数据大就替换堆顶的数据，再向下调整
                       
                    3.  
                      最后堆里面K个数就是最大的那K个数。
                       
                    时间复杂度：O(N*logK)
                     

                    这是求最大的那K个数
                     

                    求最小的那K个数则相反
                     
 
 
                    1.  
                      用前K个数建立一个K个数的大堆
                       
                    2.  
                      剩下的N-K一个数依次跟堆顶的数据进行比较
                       
                      如果比堆顶的数据小就替换堆顶的数据，再向下调整
                       
                    3.  
                      最后堆里面K个数就是最小的那K个数。
                       
                    为什么呢？
                    求最大的前K个数就是要小堆，最小的前K个就是要用大堆来算？
                     
 
                    在求最大的前K个数时，
                    假如用大堆，且大堆堆顶元素就是最大值，
                     
 
                    那么后面的值就无法进入比较，
                    只有用小堆，堆顶元素是堆中最小元素，
                     
 
                    只要后来的元素大于堆顶就和舍去原堆顶，
                    将新的元素赋给堆顶，
                     
 
                    再向下调整，使其仍是小堆，
                    再循环往复直至所有的值比较完毕。
                     
 
                    求最小的前K个数类似
                     
 

                    测试
                     

                    Heap.c
                     

                    #include "Heap.h"
void Swap(HPDataType* px, HPDataType* py)
{
	HPDataType tmp = *px;
	*px = *py;
	*py = tmp;
}
void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}
void HeapDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->capacity = hp->size = 0;
}
void AdjustUp(int* a, int child)
{
	assert(a);
	int parent = (child - 1) / 2;
	//while (parent >= 0)
	while (child > 0)
	{
		if (a[child] size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}
void HeapPush(HP* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		size_t newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = realloc(hp->a, sizeof(HPDataType)*newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}
bool HeapEmpty(HP* hp)
{
	assert(hp);
	return hp->size == 0;
}
int HeapSize(HP* hp)
{
	assert(hp);
	return hp->size;
}
HPDataType HeapTop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	return hp->a[0];
}
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

                     

                    Heap.h
                     

                    #pragma once
#include 
#include 
#include 
#include 
// 大堆
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void AdjustUp(int* a, int child);
void AdjustDown(int* a, int n, int parent);
void Swap(HPDataType* px, HPDataType* py);
void HeapInit(HP* hp);
void HeapDestroy(HP* hp);
void HeapPush(HP* hp, HPDataType x);
void HeapPop(HP* hp);
HPDataType HeapTop(HP* hp);
void HeapPrint(HP* hp);
bool HeapEmpty(HP* hp);
int HeapSize(HP* hp);

                     

                    Test.c
                     

                    #include 
#include "Heap.h"
// 在N个数找出最大的前K个  or  在N个数找出最小的前K个
void PrintTopK(int* a, int n, int k)
{
	HP hp;
	HeapInit(&hp);
	// 创建一个K个数的小堆
	for (int i = 0; i  HeapTop(&hp))
		{
			hp.a[0] = a[i];
			AdjustDown(hp.a, hp.size, 0);
		}
	}
	HeapPrint(&hp);
	HeapDestroy(&hp);
}
void TestTopk()
{
	//此处用1000000模拟数据量大的情况
	int n = 1000000;
	int* a = (int*)malloc(sizeof(int)*n);
	srand(time(0));
	for (size_t i = 0; i  

                    运行结果：
                     

                    【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第14张
                     

                    4. 堆的应用-堆排序问题
                     
 
 
                    什么是堆排序？
                     
 
                    堆排序（英语:Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆排序可以理解为选择排序。
                     
 

                    情景1：要求使用堆对数组进行升序排序
                     

                    根据你看了以上内容，我想这对你来说并不是上面难题。
                     

                    你可能会这么想：
                    • 先用数组的元素，使用前面实现的HeapPush函数，建立一个小堆
                    • 这样每次堆顶元素就是最小值
                    • 然后把堆顶元素存入另一个数组中
                    • 利用HeapPop函数删除堆顶元素
                    • 循环往复直至排序完毕

                      很好！思路是对的！那么代码怎么实现呢？

                      前文都是建立大堆，所以这里建小堆代码要进行微调：

                      把这种思路要实现的代码全部贴这了。

                      方便大家测试。

                      Heap.c
                      #include "Heap.h"
void Swap(HPDataType* px, HPDataType* py)
{
	HPDataType tmp = *px;
	*px = *py;
	*py = tmp;
}
void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}
void HeapDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->capacity = hp->size = 0;
}
void AdjustUp(int* a, int child)
{
	assert(a);
	int parent = (child - 1) / 2;
	//while (parent >= 0)
	while (child > 0)
	{
		if (a[child] size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}
void HeapPush(HP* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		size_t newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = realloc(hp->a, sizeof(HPDataType)*newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}
bool HeapEmpty(HP* hp)
{
	assert(hp);
	return hp->size == 0;
}
HPDataType HeapTop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	return hp->a[0];
}
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}
                      Heap.h
                      #pragma once
#include 
#include 
#include 
#include 
// 大堆
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void AdjustUp(int* a, int child);
void AdjustDown(int* a, int n, int parent);
void Swap(HPDataType* px, HPDataType* py);
void HeapInit(HP* hp);
void HeapDestroy(HP* hp);
void HeapPush(HP* hp, HPDataType x);
void HeapPop(HP* hp);
HPDataType HeapTop(HP* hp);
void HeapPrint(HP* hp);
bool HeapEmpty(HP* hp);
                      Test.c
                      void HeapSort(int* a, int n)
{
	HP hp;
	HeapInit(&hp);
	// 建议一个N个小堆
	for (int i = 0; i  

                      情景2：难上加难使用堆的性质·不能用堆的结沟·不能开辟新的空间的堆排序
                       

                      嗯，就这么实现了，是不是意犹未尽呢？别急，现在给这题加上一个前提，不能使用堆的结构，就是说不能像这样
                       

                      typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

                       

                      只能使用他的性质，而且不能再开辟其他的空间，空间复杂度为O(1)。
                       

                      是不是难住你了？堆的性质·不能用堆的结沟·不能开辟新的空间~
                       

                      给个提示吧：”数组是可以看作完全二叉树的，想想前面是怎么建堆的？“
                       

                      恍然大悟了吧！
                       

                      这里只需要使用AdjustUp函数，前文讲过这个函数的原理哦~
                       

                      这里是这么想的：
                      • 把前i个数视作堆
                      • 每次插入一个数，循环向上调整，也就相当于建堆了
                      • 因为我们要升序排序，所以要把大的选出来与数组最后一位交换，是不是想起了，堆顶的删除？这也是巧妙利用了它的性质。
                      • 交换后，向下调整使它仍然是大堆，再次选出最大值，循环往复直至排序完成

                        是不是很妙！

                        不过建堆的方法还有一种就是向下调整

                        • 从最后一位节点(也就是数组最后一位)的父亲开始（也就是（n-1-1）/2）

                        • 倒着调整使其自己所在的子树成为大堆

                        • 然后再找前一个节点，同样调整使其自己所在的子树成为大堆

                        • 一直往前这样下去，使其总体最终成为大堆

                          当然，方法不止一种，但是思路大差不差，你也能尝试一下更多解法

                          代码实现，这里也做了修改，变成了调大堆，所以也附上源码：

                          void Swap(HPDataType* px, HPDataType* py)
{
	HPDataType tmp = *px;
	*px = *py;
	*py = tmp;
}
void AdjustUp(int* a, int child)
{
	assert(a);
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child  a[child])
		{
			++child;
		}
		// 如果大的孩子大于父亲，则交换，并继续向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	// 把a构建成大堆
	// 方法1：
	for (int i = 1; i = 0; --i)
//	{
//		AdjustDown(a, n, i);
//	}
//
//	// 依次选数，调堆
//	// O(N*logN)
	for (int end = n - 1; end > 0; --end)
	{
		Swap(&a[end], &a[0]);
		// 再调堆，选出次小的数
		AdjustDown(a, end, 0);
	}
}
int main()
{
	int a[] = { 70, 56, 30, 25, 15, 10, 75, 33, 50, 69 };
	for (int i = 0; i  

                          只要前面插入删除会了，后面也很好理解的对吧~
                           

                          后记
                           

                          那么这一篇到这里就结束了，主要讲述二叉树的的理论及相关应用·堆排序·TOPK问题。
                           

                          下一篇将讲述二叉树链式存储，前中后序遍历，以及怎么根据前中，后中的遍历结果推出二叉树的结构，和层次遍历的实现，感谢支持，如果有什么问题，可在评论区提出！
                           

                          下一篇链接☞https://blog.csdn.net/m0_67759533/article/details/128883813
                           

                          【数据结构之二叉树简介·顺序存储·应用：堆·堆排序·TOPK问题】 第15张

相关阅读：

1、System Dashboard for Mac：强大的系统监控与管理工具

2、【JavaEE多线程】Java 文件操作

3、如何用Python构建一个生产级别的电影推荐系统 - 机器学习手册

4、【数据结构】图论（图的储存方式，图的遍历算法DFS和BFS、图的遍历算法的应用、图的连通性问题）

5、基于SSM的旅游管理系统论文

免责声明
1、本网站属于个人的非赢利性网站，转载的文章遵循原作者的版权声明。
2、本网站转载文章仅为传播更多信息之目的，凡在本网站出现的信息，均仅供参考。本网站将尽力确保所
提供信息的准确性及可靠性，但不保证信息的正确性和完整性，且不对因信息的不正确或遗漏导致的任何
损失或损害承担责任。
3、任何透过本网站网页而链接及得到的资讯、产品及服务，本网站概不负责，亦不负任何法律责任。
4、本网站所刊发、转载的文章，其版权均归原作者所有，如其他媒体、网站或个人从本网下载使用，请在
转载有关文章时务必尊重该文章的著作权，保留本网注明的“稿件来源”，并白负版权等法律责任。

手机扫描二维码访问

文章版权声明：除非注明，否则均为主机测评原创文章，转载或复制请以超链接形式并注明出处。

相关阅读

发表评论

快捷回复： 表情：
评论列表 （暂无评论，6419人围观）

还没有评论，来说两句吧...

目录[+]